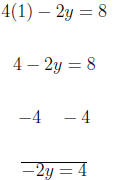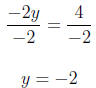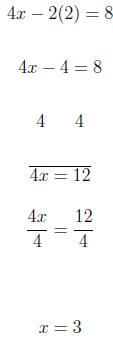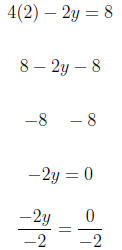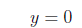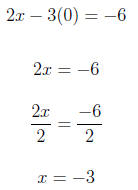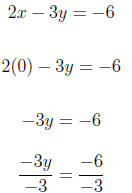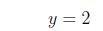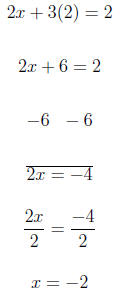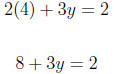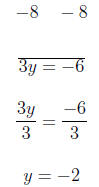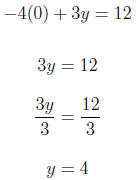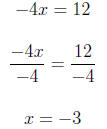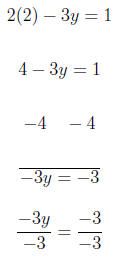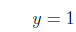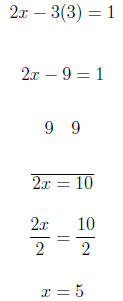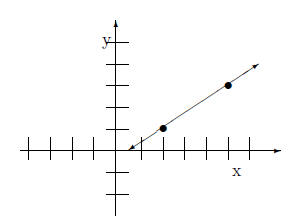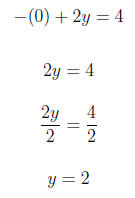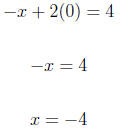|
Home |
Graphing Linear EquationsBy the end of this section, you should be able to solve
the following problems: {(?, 2), (4, ?), (?, 0)} 2. Find the intercepts of the given equation. −4x + 3y = 12 3. Graph the linear equation. Use intercepts where convenient. 2x − 3y = 1 4. Graph the linear equation. Use intercepts where
convenient. 2 ConceptsWhen we graph a linear equation we always get a line. That
means that it 2.1 Example Graph: 4x − 2y = 8. for the values: {(1, ?), (?, 2), (2, ?)} In this example, we are given 2 values for x and one value
for y, and our We substitute into the equation to find the missing value.
We begin with
For y = 2 we have
For x = 2 we have
So the set of points we have to graph are: {(1,−2), (3,
2), (2, 0)}
3 ConceptsIn our next example, we use what are called the
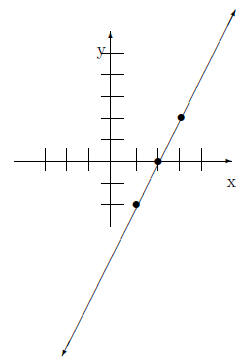
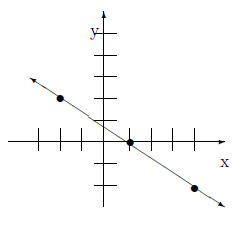
x-intercept and y-intercept to 3.1 Example Use intercepts to graph the following equation. 2x − 3y = −6 To get one x-intercept we replace y with 0. So the x-intercept is (-3,0). To find the y-intercept we
replace x with 0 So the y-intercept is (0,2). The graph is below
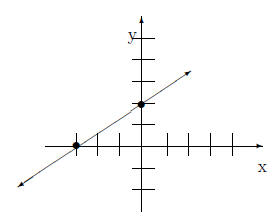
4 Facts1. The equation of the y-axis is x = 0. 5 Exercises1. Find the missing value in each coordinate pair and graph the equation. {( , 2), (4, ), ( , 0)} 2. Find the intercepts for the given equation. −4x + 3y = 12 3. Graph the linear equation. Use intercepts where convenient. 2x − 3y = 1 4. Graph the linear equation. Use intercepts where convenient. −x + 2y = 4 6 Solutions1. Find the missing value in each coordinate pair and graph the equation. {( , 2), (4, ), ( , 0)} For y = 2 we have
For x = 4
For y = 0
Therefore, we have: {(−2, 2), (4,−2), (1, 0)}
2. Find the intercepts for the given equation. −4x + 3y = 12 For x = 0
For y = 0
The intercepts are: {(0, 4), (−3, 0)} 3. Graph the linear equation. Use intercepts where convenient. 2x − 3y = 1 We substitute in x = 2 so we get a number evenly divisible
by 3 on the For x = 2
We substitute in y = 3 so we get a number evenly divisible
by 2 on the
Using (2,1) and (5,3) we graph the equation.
4. Graph the linear equation. Use intercepts where convenient. −x + 2y = 4 For x = 0
For y = 0
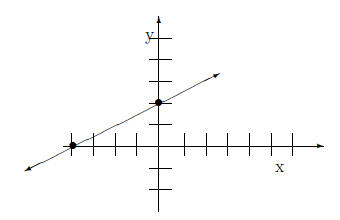
Using (0,2) and (-4,0) we graph the equation
|