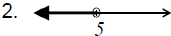Inequalities and Applications
■ Solving Inequalities
■ Interval Notation
■ The Addition Principle for Inequalities
■ The Multiplication Principle for Inequalities
■ Using the Principles Together
■ Problem Solving
Solving Inequalities
An _________ is any sentence with<, >, ≤, ≥ , or ≠ .
Examples
3x + 2 > 7, c ≤ 7, and 4x − 6 ≠ 3.
Solving Inequalities
A _______ is any value for a variable that makes an inequality
____ . The set of all solutions is called the .
Examples
| Determine whether |
Graph x < 2 and |
| 5 is a solution to |
express in set builder notation |
| 3x + 2 > 7 |
|
Interval Notation
An _________ expresses a set of numbers. They are written:
•_________________________
•_________________________ the end points from the set
Interval Notation
•_________________________ the end points from the set.
If a and b are real numbers such that a < b:
The open interval (a, b) is the set of all x’s graphed
The closed interval [a, b] is the set of all x’s graphed
The half-open interval (a, b] is the set of all x’s graphed
The interval [a, ∞ ) is the set of all x’s graphed
The interval (-∞, a) is the set of all x’s graphed
Graphs, Sets and Intervals - Practice
Graph:
1. (-2, 4]
Write each in set notation:
1. (-2, 4]
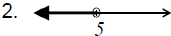
Write each in interval notation:
1. {x | 1 < x < 7}

The Addition Principle for Inequalities
For any real numbers a, b, and c:
| a < b |
a ≥ b |
| is equivalent to |
is equivalent to |
| a + c < b + c; |
a + c ≥ b + c; |
Example
Solve and graph x – 2 > 7.
The Multiplication Principle for Inequalities
| For any real numbers a, b, and for
any positive number c |
| a ≤ b |
a> b |
| is equivalent to |
is equivalent to |
| a·c ≤ b·c; |
a·c > b·c; |
| For any real numbers a, b, and for
any negative number c |
| a < b |
______________
______________
______________ |
| is equivalent to |
| a·c > b·c; |
Solve and graph, also write solution in set and interval notation.
−2(x − 5) − 3x ≤ 4x − 7
Problem Solving
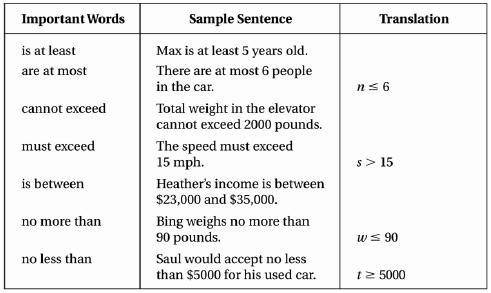
Translation
Tom’s construction work can be paid to him in two ways:
Plan A: $300 plus $9 per hour or
Plan B: Straight $12.50 per hour.
If the job takes n hours,
what is the value of n so that Plan B is better for Tom.
Intersections, Unions, and
Compound Inequalities
■ Intersection of Sets and Conjunctions of
4.2
Sentences
■ Unions of Sets and Disjunctions of Sentences
■ Interval Notation and Domains
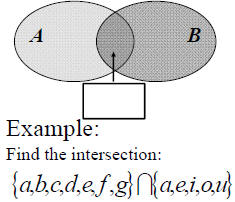
Intersection and Conjunction
The ____________ _ of two sets
A and B is the set of all elements
that are common to both A and B.
Intersection is written as ______
A _______________is two or more
sentences are joined by _________.
Ex: a conjunction of inequalities
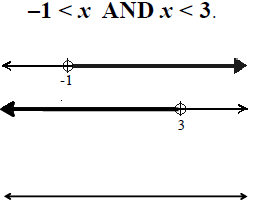
Example:
Solve and graph and state answer as an interval:
2x +1≥ −3 and −3x > −12
Mathematical Use of “and”
________________________________________
of these ideas to the symbol ___
Any solution of an intersection must make every part true |
Note that for a < b,
_______________ b > x and x > a
______________ can be abbreviated
______________ b > x > a
3 < 2x +1 < 7 is the same as 3 < 2x +1 and 2x + 1 < 7
Union and Disjunction
The of two sets A or B
is the combination of all elements
contained in both A and/or B.
Union is written as _________
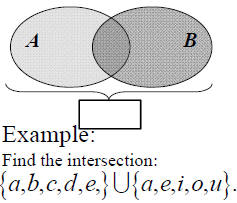
A is two or more
sentences are joined by _______.
Ex: a disjunction of inequalities
Mathematical Use of “or”
_______________________________________
of these ideas to the symbol ___
A solution to a union makes part of the it true |
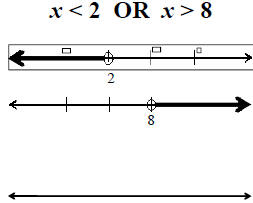
Example Solve and graph:
2x +1≥ 3 or 3x < −3.
|