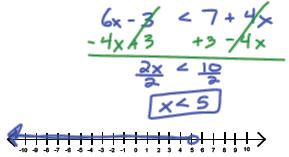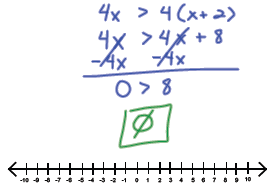Solving Inequalities
Property of Comparisons
For all real numbers a and b, one and only one of the
following statements is true:
a < b, a = b, or a > b

Suppose you know two facts about the graphs of
three numbers a, b, and c.
1) The graph of a is to the left of the graph of b:
a < b
2) The graph of b is to the left of the graph of c:
b < c
From the graph above, you can see that the graph
of a is to the left of the graph of c: a < c
Transitive Property of Order
For all real numbers a, b, and c:
1) If a < b and b < c, then a < c.
2) If c > b and b > a, then c > a.
What happens when the same number is added
or subtracted to each side of an inequality?
3 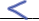 6 6
3  6 6
3 + 4 _____ 6 + 4
3 - 4_____ 6 - 4
7 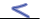 10 10
-1 2 2
Addition Property of Order
For all real numbers, a, b and c:
1) If a < b, then 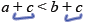
2) If a > b, then a + c > b + c
What happens when the same number is
multiplied on each side of an inequality?
4  -3 -3
4  -3 -3
4(2) _____ -3(2)
4(-2)_____ -3(-2)
8 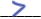 -6 -6
-8 6 6
Multiplication Property of Order
For all real numbers a, b, and c such that
| c > 0 (c is positive): |
c < 0 (c is negative) |
| 1) If a < b, then ac < bc |
 |
| 2) If a > b, then ac > bc |
 |
What would happen if we multiplied
both sides of an inequality by 0?
Example 1: Solve the inequality.

Example 2: Solve 6x - 3 < 7 + 4x and graph the
solution set.
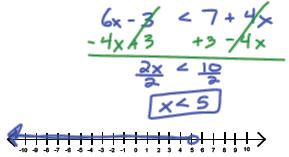
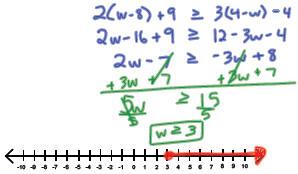
Example 3: Solve 2(w - 8) + 9 ≥ 3(4 - w)- 4
and graph its solution set.
Example 4: Solve 4x > 4 (x + 2)
and graph its solution set.
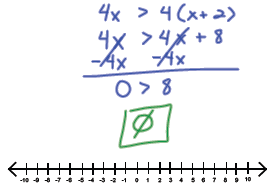
Example 5: Solve y + 5 < 7y - 6(y - 1)
and graph its solution set.

|



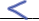 6
6  6
6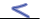 10
10  2
2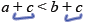
 -3
-3 -3
-3 -6
-6 6
6