|
|
Solving Inequalities
I. Solving Inequalities
To solve an inequality, apply the equation solving techniques of: “Get rid of”
1. Parentheses by using the distributive property.
2. Denominators: Multiply each side of equation by common denominator.
Decimals: Multiply each side of equation by 10, 100, 1000, etc.
3. Like terms on the same side by combining
Goal: The equation should be no more complicated than: 4x – 8 = -7x + 9
4. Signs (addition or subtraction) by using the addition principle (add
opposites).
Get variable terms on one side of the equation and all constant terms on the
other side.
Goal: The equation should be no more complicated than: 4x = -9
5. Coefficients by dividing by coefficient (BY SAME NUMBER). Goal: x = number
Two additional rules must be applied when solving an inequality:
1. When you multiply or divide an inequality by a negative number your must
reverse the
inequality symbol.
2. The variable must be on the left.
Use these rules to solve the following inequalities:
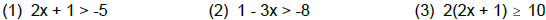
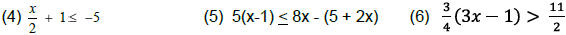
You Try: 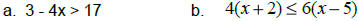
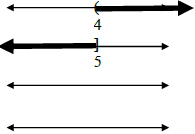
B. Three Forms of a Solution
Complete the following chart, remembering that < and > are represented by
parentheses while
≤ and ≥ are represented by brackets Interval is always expressed from LEFT to
RIGHT (smallest to largest value). And use the symbols ∞ and −∞ to represent
infinity
and negative infinity.
| Solution |
Set Builder Notation |
Number Line |
Interval Notation |
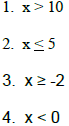 |
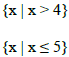 |
 |
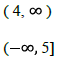 |
C. Determine whether the given number is a solution.
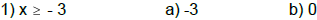
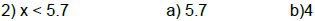
Solve the following inequalities and express the solution
on a number line.
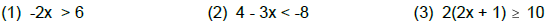

|