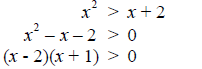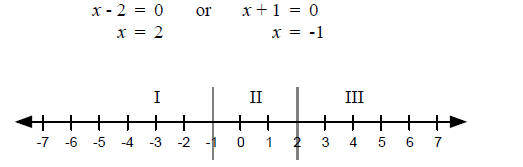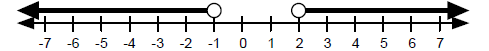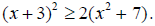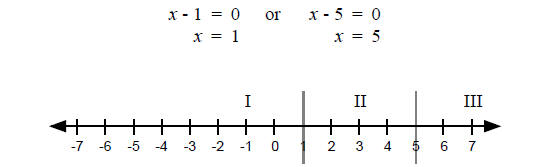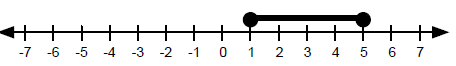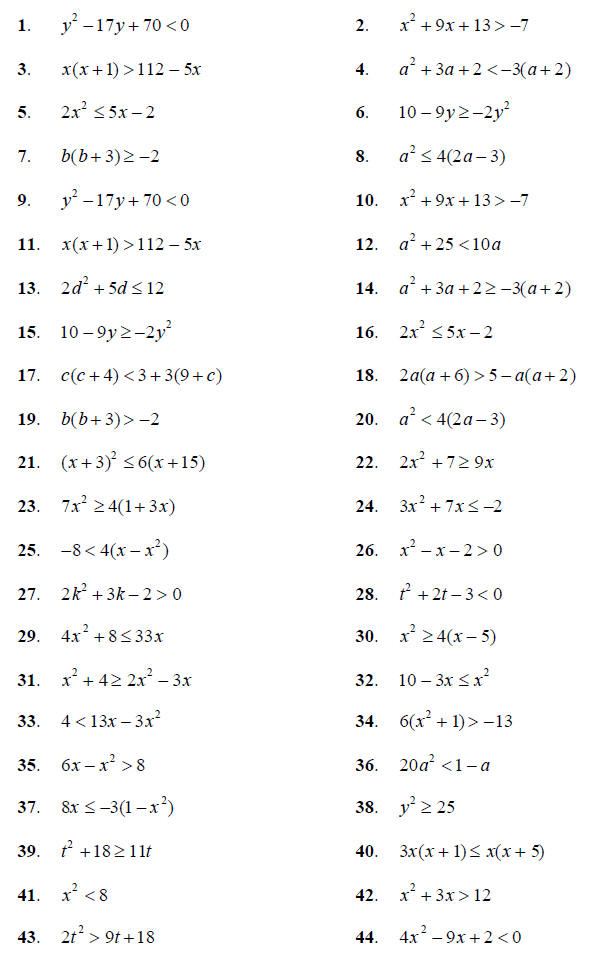|
Home |
QUADRATIC INEQUALITIESDefinition Quadratic inequalities in one variable are
inequalities which can be written in one of
Procedure Solving Quadratic Inequalities 1. Move all terms to one side. Example 1 Solve the inequality, x^2 > x + 2 . Solution
The corresponding equation is (x - 2)(x + 1) = 0 so…
Now we test one point in each region.
So the solution to this inequality is x < -1 or x > 2. Example 2 Solve the inequality,
Solution
The corresponding equation is (x - 1)(x - 5) = 0 so…
Now we check one point in each region.
So the solution to this inequality is 1 ≤ x ≤ 5. §4-2 PROBLEM SETSolve each quadratic inequality, and graph the solution on a number line.
§4-2 PROBLEM SOLUTIONS
|
||||||||||||||||||||||||||||||||


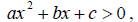
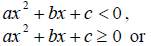
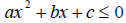 where a, b and c are
real numbers.
where a, b and c are
real numbers.