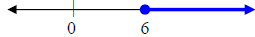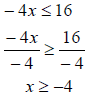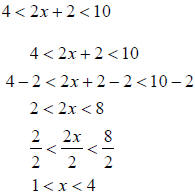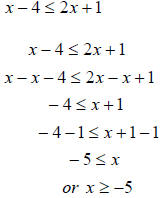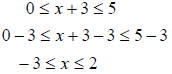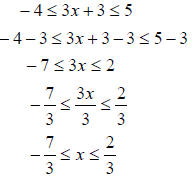|
Home |
InequalitiesDefinitions Rational Numbers: A number that can be expressed as
the quotient of two integers Example 1 Identify each number as rational or
irrational Inequalities > Greater than The number line Solving Inequalities Inequality Properties Transitive Property a > b and b > c
Addition Property for Inequalities a > b
Multiplication properties for Inequalities (If c is positive, then a > b
Subtraction property for Inequalities a > b
Example 2 Solve the following inequality 2x + 4 >10
Example 3 Solve the following inequality 12x + 36 ≤ 6x + 48
Example 4 Solve the following inequality
Compound Inequalities Example 5 Solve Example 6 Solve Example 7 Solve the following inequality 0 ≤ x + 3 ≤ 5
Example 8 Solve the following inequality − 4 ≤ 3x + 3 ≤ 5
|


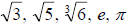
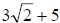 (This number is irrational)
(This number is irrational)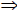 a > c
a > c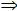 a + c > b + c
a + c > b + c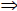 ac > bc, c > 0 )
ac > bc, c > 0 )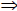 ac < bc, c < 0
)
ac < bc, c < 0
)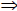 a − c > b − c
a − c > b − c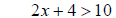
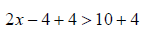 add to both sides
add to both sides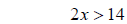 simplify
simplify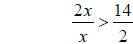 divide by 2
divide by 2 simplify
simplify
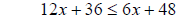
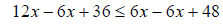 subtract x from both sides
subtract x from both sides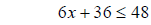 simplify
simplify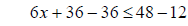 substract 36 from both sides
substract 36 from both sides
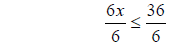 divide by 6
divide by 6