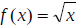Home
Linear Equations and Inequalitie
Solving Inequalities
Absolute Value Inequalities
Graphing Equivalent Fractions Lesson Plan
Investigating Liner Equations Using Graphing Calculator
Graphically solving a System of two Linear Equatio
Shifting Reflecting Sketching Graph
Graphs of Rational Functions
Systems of Equations and Inequalities
Graphing Systems of Linear Equat
LINEAR FUNCTIONS: SLOPE, GRAPHS AND MODELS
Solving Inequalities with Absolute Values
Solving Inequalities
Solving Equations & Inequalities
Graph the rational function
Inequalities and Applications
Inequalities
Using MATLAB to Solve Linear Inequalities
Equations and Inequalities
Graph Linear Inequalities in Two Variables
Solving Equations & Inequalities
Teaching Inequalities:A Hypothetical Classroom Case
Graphing Linear Inequalities and Systems of Inequalities
Inequalities and Applications
Solving Inequalities
Quadratic Inequalities
Inequalities
Solving Systems of Linear Equations by Graphing
Systems of Equations and Inequalities
Graphing Linear Inequalities
Inequalities
Solving Inequalities
Solving Inequalities
Solving Equations Algebraically and Graphically
Graphing Linear Equations
Solving Linear Equations and Inequalities Practice Problems
Graphing Linear Inequalities
Equations and Inequalities
Solving Inequalities

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

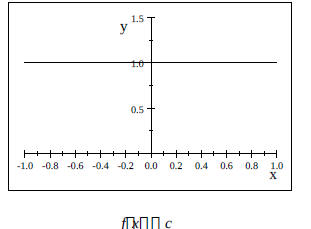
Shifting Reflecting Sketching Graph

Graphs of Commonly Used Functions in Algebra

a.) Constant Function

b.) Identity Function

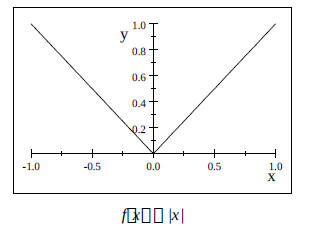
c.) Absolute Value Function

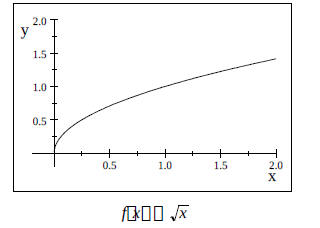
d.) Square Root Function

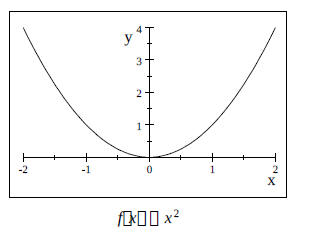
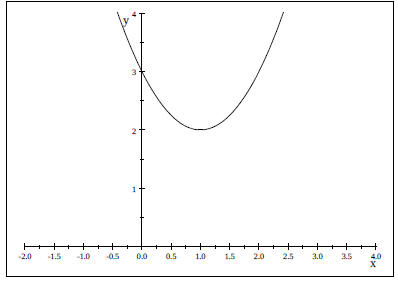
e.) Quadratic Function

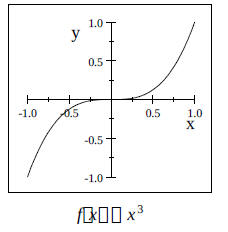
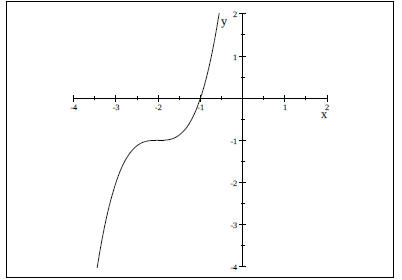
f.) Cubic Function

Most graphs of functions can be made by transforming (shifting, stretching, shrinking, reflecting) or
combining these common graphs.

Vertical and Horizontal Shifts

Let c be a positive real number. Vertical and horizontal shifts in the graphs of y = f(x) are represented
as follows:

1.) Vertical shift c units upward -> h(x) = f(x) + c
2.) Vertical shift c units downward -> h(x) = f(x) – c
3.) Horizontal shift c units to the right -> h(x) = f(x – c)
4.) Horizontal shift c units to the left -> h(x) = f(x + c)

Reflections in the Coordinate Axes

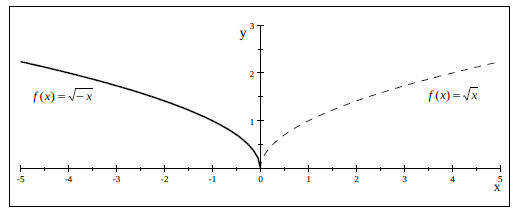
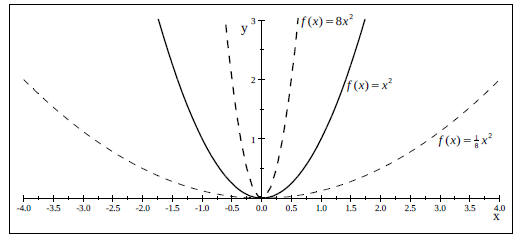
Reflections in the coordinate axes of the graph of y = f(x) are represented as follows:
1.) Reflection in the x-axis -> h(x) = -f(x)
2.) Reflection in the y-axis -> h(x) = f(-x)

Nonrigid Transformations

1.) A vertical stretch in the graph -> y = cf(x) where c > 1
2.) A vertical shrink in the graph -> y = cf(x) where 0 < c < 1
3.) A horizontal shrink in the graph -> y = f(cx) where c > 1
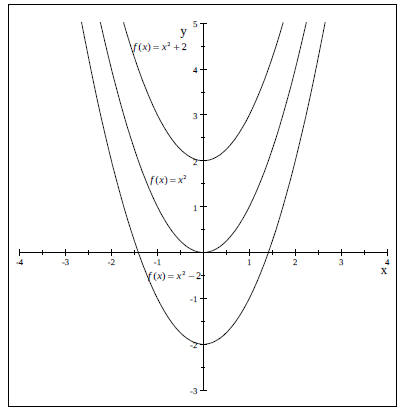
4.) A horizontal stretch in the graph -> y = f(cx) where 0 < c < 1

Vertical Shifts in the Graph of f (x) = x^2 .

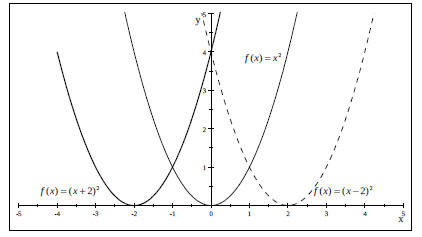
Horizontal Shifts in the Graph of f (x) = x^2 .

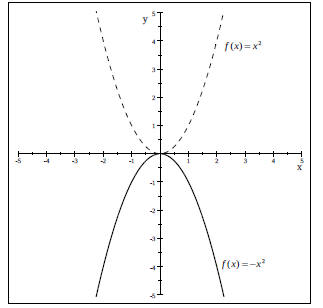
Reflection in the x-axis of the Graph of f (x) = x^2 .

Reflection in the y-axis of the Graph of

Vertical Stretches and Shrinks of the Graph of f (x) = x^2 .

Horizontal Stretches and Shrinks of the Graph of f (x) = x^2 .

Identify the common function and describe the transformation shown in the graph. Write an
equation for the graphed function.
a.)

Solution:

b.)

Solution: