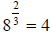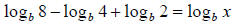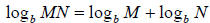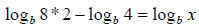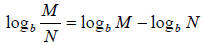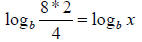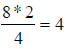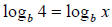Linear Equations and Inequalities
Linear Equations and Inequalities
Definition: A linear equation in one variable is any equation that can be
written in the form
ax + b = 0
If the equality symbol (=) is replaced by >, <, ≥ or ≤ , the resulting
expression is called a
linear inequality.
Example:
3x − 8 = 23 is a linear equation.
3x − 8 > 23 is a linear inequality.
Theorem: An equivalent expression will result if
a) The same quantity is added to or subtracted from each side of a given
equation.
b) Each side of a given equation is multiplied by or divided by the same nonzero
quantity.
Example:
The linear equation
3x − 8 = 23
is equivalent to (adding 111 to both sides)
111 + 3x − 8 = 23 +111
and to (multiplying by 2 on both sides)
2 * (3x − 8) = 2 * 23
However be careful…..

Let’s check that for x = 1:
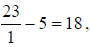 while while
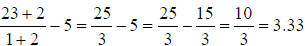
Also:
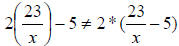
Solving a Linear Equation.

During the 2006 MLB season Alex Rodriguez
hit 35 homeruns. According to some estimates
Rodriguez may double that number in the 2008
season.
How many homeruns (x) did you expect
Rodriguez to hit this season?
He is going to double the number of homeruns of 2006, hence:
35*2 = x
70 = x
Some people argue that Rodriguez will hit a quarter of his homeruns with the
bases empty, half
of his homeruns with one man on base and the rest with the bases loaded. How
many RBIs will
Rodriguez get out of his homeruns? [Note to those of you that don’t follow
baseball: a homerun
with the bases empty counts as one RBI, a homerun with one man on base counts as
two RBIs
and a homerun with the bases loaded counts as four RBIs].
Step 1. What is a quarter?
A quarter is 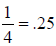 , we divide something in four
parts and each part is a quarter. , we divide something in four
parts and each part is a quarter.
Example: x/4
Step 2. What is a half?
A half is , we divide something in two parts
and each part is a half. , we divide something in two parts
and each part is a half.
Example: x/2
Step 3. Analyze your problem:
A. We have a quarter of 70, that is (70/4 )of homeruns with the bases
empty: ) 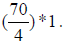
B. We have a half of 70, that is (70/2 ) of homeruns with one man on base: )
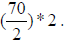
C. We have a quarter of 70, that is (70/4) of homeruns with the bases
loaded: ) 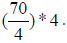
Step 4. Setup up your problem:
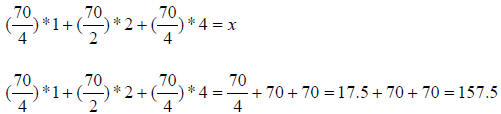
Alex Rodriguez joined the Boys and Girls Clubs of Miami in
1982. There he “developed” as a
baseball player. Now he wants to repay the Club. The Club has created the event
Alex Rodriguez
Evening with the All Stars. Each ticket for the event has a cost of $ 400
dollars. It is estimated
that for each homerun that Rodriguez hits he will sell two tickets for the
event. In top of that
Rodriguez is going to donate $ 20,000 dollars of his own money to the Club. The
goal of the
Club is to raise $ 100,000 dollars. How many homeruns are necessary in order to
reach the $
100,000 dollars goal?
Step 1. Analyze your problem:
A. We have 20,000 even if we don’t sell one ticket.
B. For each homerun (x) we sell two tickets at 400 dollars per ticket, that is:
x *2*400.
C. We need 100,000 dollars.
Step 2. Setup your problem:
20,000 + x * 2 * 400 = 100,000
Step 3. Subtract 20,000 from both sides, and multiply 2*400 = 800:
x *800 = 80,000
Step 4. Divide both sides by 800.
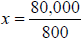 or also, x = 100. or also, x = 100.
According to our previous estimation, Is the Club going to
reach the goal?
70 < 100 , not likely.
On your own….

Bill Gates, arguably the world's richest man,
wants to buy a new house. In total he wants
to spend $ 20,000,000 dollars. Given that
there is a sale tax of 5 percent, how much
should Bill Gates pay for the house?
Step 1. What is the 5 percent of something?
5 percent of x = x *.05.
For instance:
15 percent of 30 = 30*.15 = 4.50.
Step 2. Analyze your problem.
Step 3. Setup your problem.
Theorem: An equivalent inequality will result and the sense or direction will
remain the
same if each side of the original inequality
a) Hast the same real number added or subtracted from it.
b) Is multiplied or divided by the same positive number.
An equivalent inequality will result and the sense of direction will reverse if
each side of the
original inequality
c) Is multiplied or divided by the same negative number.
Example:
70 < 100 , multiply by 2 and you get: 140 < 200
However…
70 < 100 , multiply by - 1 and you get: − 70 > −100
Definition: The double inequality a < b < c indicates that a < b and b < c , and
of course
a < c .
CAREFUL WITH TABLE 1. For our purposes we will use:
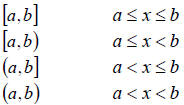
Definition: The symbol ∞ represents infinity, or an
interval that continues indefinitely to
the right, while the symbol − ∞ represents an interval that continues
indefinitely to the left.
The interval (− ∞,∞) is the entire real number line. You should not use a “[ or
]” next to
the infinity symbol.
Thus we can write

Example:
2 ≤ x ≤ 8is equivalent to [2,8]
1< x <10is equivalent to (1,10)
x > 8is equivalent to (8,∞)
x ≥10is equivalent to [10,∞)
Solving a Linear Inequality.

The recent presidential primary election for the
Democratic Party was a close one. Before one of
the contests the numbers suggested that Hillary Clinton was ahead in that state
with 45 % of the
votes. Obama was in second place with 30 % of the votes. Finally, John Edwards
was in third
place with 25 % of the votes.
Obama was expecting Edwards to drop the race before election day. If this is
true, what
percentage of Edwards’s votes does Obama needs in order to win the election?
Step 1. Analyze your problem:
A. Edwards has 25 % of the votes.
B. Clinton has 45 % of the votes, so Obama needs more than 45 % of the votes to
win the
primary election.
C. There is a fraction of Edward’s votes (x) that will go to Obama and another
fraction (1-x)
that will go to Clinton.
Step 2. Setup your problem.
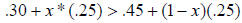
Step 3. Expand the parenthesis.

Step 4. Add .45 and .25.
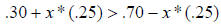
Step 5. Subtract .30 from both sides.
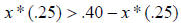
Step 6. Add x * (.25) to both sides.
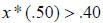
Step 7. Divide both sides by .50.
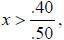 or also or also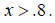
What percentage of Edward’s votes do Obama needs to get in
order to finish tied with Clinton?
x = .8, in percentage terms, 80 percent.
On your own….
The housing bubble is over. During the last
year housing prices in the U.S. have been
decreasing. However, this has not been the
case for the State of Texas. Housing prices
in Texas have been increasing for the last 6
years. The following table indicates the
change in housing prices in Texas over the
last six years. Given that the value of a
house in the year 2005 was 300,000 dollars,
How much did you had to pay for that house
in the year 2006? What is the least that you
are going to pay for that house in the year
2007 assuming that the increase in housing
prices during the year 2007 is non-negative?
What is a non-negative number?
x≥0
| Year |
Change
in price |
| 2000 |
5.96 |
| 2001 |
6.70 |
| 2002 |
3.52 |
| 2003 |
3.14 |
| 2004 |
2.92 |
| 2005 |
4.88 |
| 2006 |
6.72 |
On your own…
Problem 62 page 12 (Handout or Chapter 1, 11th edition) (assume
that it takes one day to
clean the carpet).
On your own…Home
Problems 1 – 40 page 11 (Handout or Chapter 1, 11th edition).
Graphs and Lines.
Definition:
In the Cartesian Coordinate System we have two real number lines, one horizontal
and one
vertical. The two lines cross through their origins. The ordered pair (a,b)
gives the
coordinates of a point. The first coordinate (a) is called the abscissa (x-axis)
and the second
coordinate (b) is called the ordinate (y-axis).
Example:
Let’s plot some coordinates…
(3,3) (-2,5) (2,-5) (-4,-4)
Now let’s plot a line…
20x −10 y = 5
First solve for y:
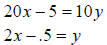
Now construct a table:
| x |
y |
|
| 0 |
-.5 |
Intercept for y |
| 1 |
1.5 |
|
| 2 |
3.5 |
|
| 3 |
.25 |
|
| .25 |
0 |
Intercept for x |
On your own…Home
Plot this: 27x − 9y = 3
Definition: The ratio of the change in y to the change in x as the point
moves from point 1
to point 2 is called the slope of the line. If a line passes through two
distinct points P (x1 , y1)
and P (x2 , y2) then the slope is
given by
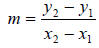
Example:
Using the table:
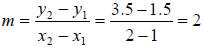
Interpretation:
“If we increase x by 1, then y increases by 2.”
See Table 1, page 18 (Handout or Chapter 1, 11th edition).
See Example 7, page 21 (Handout or Chapter 1, 11th edition).
On your own…
Problem 62, page 27 (Handout or Chapter 1, 11th
edition).
See Example 3, Page 31 (Handout or Chapter 1, 11th edition).
On your own…Home
Problem 12, page 38 (Handout or Chapter 1, 11th edition).
Functions
Definition: A function is a correspondence between two sets of elements such
that to each
element in the first set there corresponds one and only one element in the
second set. The
first set is called the domain, and the set of corresponding elements in the
second set is
called the range.
In the first chapter we learned about linear functions (lines), but not all
functions are linear.
Other types of functions (e.g. quadratic) are more difficult to graph. In this
case we need to use
point-by-point plotting.
Solving a Non-linear Equation.
In the first chapter we had things like:
y = 9 − x
| x=1 |
x=2 |
x=3 |
x=4 |
x=5 |
x=6 |
| 8 |
7 |
6 |
5 |
4 |
3 |
We can find a lot of the points, but we only need two
points to sketch the graph. It’s just a line!!!
Now with other types of equations in not that easy. See for example the
following quadratic
equation:
y = 9 − x2
| x=1 |
x=2 |
x=3 |
x=4 |
x=5 |
x=6 |
| 8 |
5 |
0 |
-3 |
-5 |
-27 |
Definition: A square root of a number x is a number a
such that a2 = x , or a number a,
whose square (the result of multiplying the number by itself) is x. Every
non-negative real
number x has a unique non-negative square root, denoted with a radical symbol as
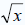 . For . For
example, the square root of 9 is 3, denoted 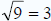 ,
because 32 = 3*3 = 9 . Square roots often ,
because 32 = 3*3 = 9 . Square roots often
arise when solving quadratic equations, or equations of the form: ax2
+ bx + c = 0, due to
the variable x being squared.
On your own…

During the 2002-2003 season, while playing
with the Orlando Magic, Tracy McGrady
averaged 32.1 points per game. Last season
with the Houston Rockets, McGrady
averaged only 24.6 points per game.
McGrady is worry about his performance.
He knows that his points per game depend
on the number of hours that he spends
practicing for a game. Assume that the
following equation provides the relationship
between points (y) and practice hours (x).
y2= x +1016
Using a graph estimate how many hours McGrady needs to
practice in order to score 32 points
per game.
Step 1. Solve for y:
Step 2. Setup a table:
However, points are not the only worry for McGrady. In the
year 2002-2003 he averaged 2.6
turnovers per game. Last season he averaged 3 turnovers per game. Assume that
the following
equation provides the relationship between turnovers (y) and practice hours (x).
y * x2= 94
Using a graph estimate how many hours McGrady needs to practice in order to make
only 2.61
turnovers per game.
Step 1. Solve for y:
Step 2. Setup a table:
See Table 1, Table 2 and Table 3 in page 49 (page 7, 10th
edition).
Definition: any variable used as a placeholder for domain values is called an
independent
variable (x in our examples), while any variable that is used as a place holder
for range
values is called a dependent variable (y in our examples).
Definition: if in a equation in two variables (e.g. x and y), we get exactly one
output (value
for the dependent variable) for each input (value for the independent variable),
then the
equation specifies a function. The graph of such a function is just the graph of
the
specifying equation. If we get more than one output for a given input, the
equation does
not specify a function.
Definition: each positive real number has two square roots,
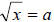 (which is called the (which is called the
principal square root) and  (the negative of
the principal square root). For (the negative of
the principal square root). For
instance, 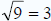 and and
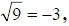 , this because while (3)*(3) = 9, we
also have that , this because while (3)*(3) = 9, we
also have that
(−3) * (−3) = 9 .
Example:
Let’s go back to our Tracy McGrady example:
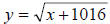
When x = 8
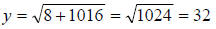
But since (-32)*(-32) = 1024 we also have that
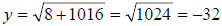
In general, we can write this as
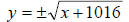
Is this equation a function? Since each positive real
number has two square roots to each input
value of x there corresponds two output values (
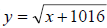 and and 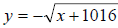 ). Thus, this
). Thus, this
equation does not specify a function.
Using Function Notation
In general we are going to use the letter f (guess why?) to refer to a function.
But we can use any
letter (m, k, g, etc.).
Let’s say that we have
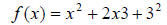
We can evaluate this function at 2 and 4:

In general:

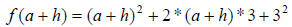
It is also common to express an equation like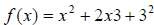 as f (x) = (x + 3)2 . Let’s
as f (x) = (x + 3)2 . Let’s
verify that:
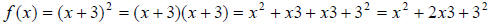
On your own…
Given the following equation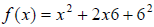 estimate the
following: estimate the
following:
f (8) − f (3) − f (1)
Definition: if a function is specified by an equation
and the domain is not indicated, then we
assume that the domain is the set of all real numbers replacements of the
independent
variable that produces real values for the dependent variable. However, a domain
may be
implicit or suggested by a specific problem. For instance, if the problem
mentions prices,
we know that prices are always a non-negative number or [0,∞) , (another example
is
points in a basketball game). The range is the set of all outputs (dependent
variable)
corresponding to the input variables.
See Figure 6, page 53 (page 10, 10th edition).
Finding a Domain
Let’s say that we have the following equation:

For y to be real, 10 – x must be greater than or equal to
zero.
10 − x ≥ 0
10 ≥ x or the same x ≤ 10.
Hence the domain is (−∞,10].
On your own…Home
Problems 1 – 20 page 59 (Problems 1 to 12, page 17, 10th edition).
Problems 21 – 30 page 59 (Problems 19 to 26, page 18, 10th
edition).
Problems 65 – 70 page 60 (Problems 39 to 44, page 18, 10th
edition).
On your own…
Problem 128 page 63 (Problem 90, page 21, 10th edition).
Elementary Functions: Graphs and Transformations.
A function can be express as a function of another function. Not that confusing.
For instance:
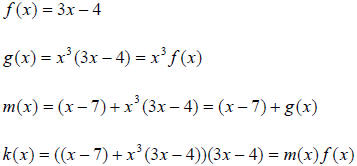
Definition: we have a set of basic elementary functions
| f (x) = x |
Identity Function. |
| h(x) = x2 |
Square Function. |
| m(x) = x3 |
Cube Function. |
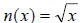 |
Square Root Function. |
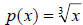 |
Cube Root Function. |
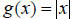 |
Absolute Value Function. |
Now let’s evaluate each function at 10 and – 10.
| f (10) = 10, f (−10) = −10 |
Same number different sign. |
| h(10) = 100, h(−10) = 100 |
Same number. |
| m(10) = 1000,m(−10) = −1000 |
Same number different sign. |
| n(10) = 3.16, n(10) = not a real number. |
Big difference. |
| p(10) = 2.1544, p(−10) = −2.1544 |
Same number different sign. |
| g(10) = 10, g(−10) = 10 |
Same number. |
See Figure 1, page 65 (page 23, 10th
edition).
Vertical and Horizontal Shifts
You can shift a function vertically or horizontally.
For the function
f (x) =l xl
g(x) = lx l+ 5 and g(x) =l xl − 5 are vertical shifts, while
g(x) = lx + 5l and g(x) = lx − 5l are horizontal shifts.
See Summary in page 69 (page 27, 10th edition).
On your own…Home
Problems 1 – 28 page 73 (problems 1 to 28, page 32, 10th edition).
Problems 37 – 40 page 73 (problems 37 to 42, page 32, 10th edition).
Problems 43 - 48 page 73 (problems 43 to 48, page 33, 10th edition).
Quadratic Functions.
Definition: If a, b, and c are real numbers with a ≠ 0 , then the function f
(x) = ax2 + bx + c
is a quadratic function and its graph is a parabola.
Definition: The most popular method (there are other
ways!!!) for obtaining the x
intercepts of a quadratic equation is the quadratic formula
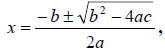 where b2 −
4ac ≥ 0 . where b2 −
4ac ≥ 0 .
Example:
If we have f (x) = 2x2 + 6x + 4 , then a = 2, b = 6 and c = 4,
therefore:
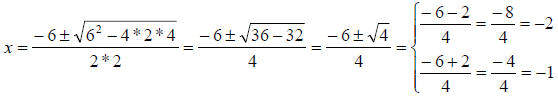
Let’s verify that:
2(−1)2 + 6(−1) + 4 = 2 − 6 + 4 = 0 and 2(−2)2 + 6(−2) + 4
= 8 −12 + 4 = 0 .
Definition: a polynomial function is a function that can be written in the
form
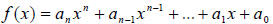
For an nonnegative integer, called the degree of the polynomial. The
coefficients
a0 , a1 ,..., an are real numbers with an≠
0. The domain of a polynomial function is the set of
all real numbers.
Definition: a rational function is any function that can be written in the form
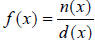
Where n(x) and d(x) are polynomials. The domain is the
set of all real numbers, such that
d(x) ≠ 0.
A rational function has at most one horizontal asymptote. The graph of a
rational function
approaches the rational asymptote (when one exists) both as x increases and
decrease without
bound (it gets closer and closer without touching).
On your own…
Problems 1 to 4 page 90 (problems 1 to 4, page 64, 10th editio
Exponential Functions.
Definition: The equation f (x) = bx , b > 0,b ≠ 1, defines an
exponential function for each
different constant b, called the base. The domain of f is the set of all real
numbers, and the
range of f is the set of all positive real numbers.
Example:
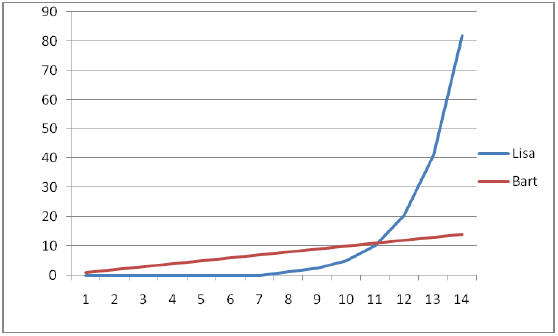
Homer Simpson is offering Bart and Lisa two choices for an increasing weekly
allowance: the
first option begins at 1 cent and doubles each week, while the second option
begins at $1 and
increases by $1 each week. Bart argues that the second option, growing at a
constant rate of
$1/week, pays more and is obviously better. However, Lisa thinks that the first
option will
eventually grow much larger and selected this option. What did you think?

| Week |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| Lisa |
1c |
2c |
4c |
8c |
16c |
32c |
64c |
$1.28 |
$2.56 |
$5.12 |
$10.24 |
$20.48 |
$40.96 |
$81.92 |
$163.84 |
$327.68 |
$655.36 |
$1310.72 |
$2621.44 |
| Bart |
$1 |
$2 |
$3 |
$4 |
$5 |
$6 |
$7 |
$8 |
$9 |
$10 |
$11 |
$12 |
$13 |
$14 |
$15 |
$16 |
$17 |
$18 |
$19 |
For Lisa, the allowance at week n is 2n cents;
thus, at week 15 the payout is 215 = 32768c = $327.68. All formulas
of the form kn,
where k is an unchanging number greater than 1 (e.g., 2), and n is the amount of
time elapsed, grow exponentially. For Bart, the
payout at week n is simply n + 1 dollars. The payout grows at a constant rate of
$1 per week.
Here is a graph of the first 14 weeks.
Definition: The base
 is the most popular of
bases. The base is the most popular of
bases. The base  is an irrational is an irrational
number, that is, it cannot be represented exactly by any finite decimal
fraction.
However,  can be
approximated as closely as we like by evaluating the expression can be
approximated as closely as we like by evaluating the expression
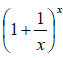
for a sufficiently large x. In general
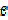 = 2.71828 18284 59045
23536........ = 2.71828 18284 59045
23536........
| Number of known decimal digits of
e |
| Date |
Decimal digits |
Computation performed by |
| April 27 2007 |
100,000,000,000 |
Shigeru Kondo & Steve Pagliarulo |
| July 16 2000 |
3,221,225,472 |
Colin Martin & Xavier Gourdon |
| November 21 1999 |
1,250,000,000 |
Xavier Gourdon |
| October 1999 |
869,894,101 |
Sebastian Wedeniwski |
| September 1997 |
50,000,817 |
Patrick Demichel |
| August 1997 |
20,000,000 |
Birger Seifert |
| 1994 |
10,000,000 |
Robert Nemiroff & Jerry Bonnell |
| 1949 |
2,010 |
John von Neumann (on the ENIAC) |
| 1748 |
18 |
Leonhard Euler |
Some rules of exponents:
1.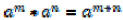
If the bases of the exponential expressions that are multiplied are the same,
then you can
combine them into one expression by adding the exponents.
This makes sense when you look at:
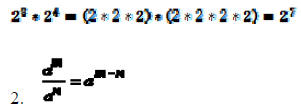
If the bases of the exponential expressions that are
divided are the same, then you
can combine them into one expression by subtracting the exponents.
This makes sense when you look at:
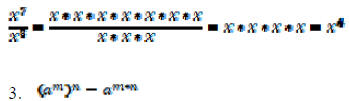
When you have an exponential expression raised to a power,
you have to multiply
the two exponents.
This makes sense when you look at:
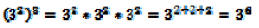
Notice that we had to use another rule of exponents to
help us make sense of this
rule. This is a common occurrence. Many times you will use more than one rule
of exponents when working problems.
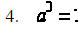
Any number or variable raised to the zero power is always
equal to 1.

It is important to note that if a negative exponents
already appears in the
denominator of a fraction, then it will move to the numerator as a positive
exponent. In short, a negative exponent changes the location (numerator or
denominator) of an expression and changes the sign of the exponent.
On your own…
Problems 15 – 20 page 103 (problems 15 to 20, page 106, 10th
edition).
Compound Interest Rate Formula
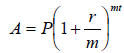
A = amount (future value) at the end of t years.
P = principal (present value).
r = annual rate, expressed as a decimal.
m = number of compounding periods per year (e.g. for quarterly m = 4).
t = time in years.
Example:

Tony Soprano has two investment
options. He can put $ 20,000 in the
gambling business in New Jersey or he
can put the $ 20,000 in an investment
account in Bank of America. By
experience Tony knows that he will get
about 40,000 back from the gambling
business in five years. He is not sure
about the investment account. It looks
too complicated for him. The only thing
that he knows is that the account pays 10
% compounded monthly. Using the
Compound Interest Rate Formula, can
you help Tony?
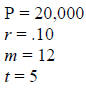
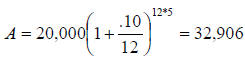
On your own…
Problem 65 page 104 only a and b (problem 67, page 107, 10th
edition).
Definition: If f is a one-to-one function, then the
inverse of f is the function formed
by interchanging the independent and dependents variables for f. Thus, if (a, b)
is a
point on the graph of f, then (b, a) is a point on the graph on the inverse of
f.
Definition: Logarithmic functions are the inverse of exponential functions, and
exponential functions are the inverse of logarithmic functions. In specific:
Logarithmic form: 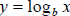
Exponential form: x = by
Example:
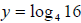 the exponential form is 16 = 4y ,
which by the way implies that y = 2. the exponential form is 16 = 4y ,
which by the way implies that y = 2.
Theorem: If b, M and N are positive real numbers, b ≠ 1, and p and x are real
numbers, then
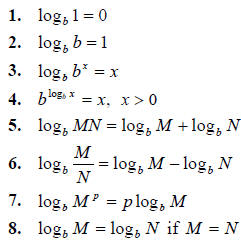
Example:
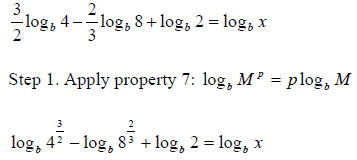
Step 2. Simplify the equation:
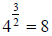 and and
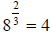
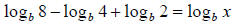
Or also:

Step 3. Apply property 5: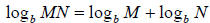
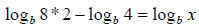
Step 4. Apply property 6: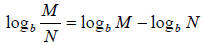
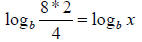
Step 5. Simplify the equation: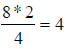
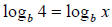
Step 6. Cancel the logs
4 = x
Definition: Common logarithms (logs) are logarithms with base 10. Natural
logarithms (LN) are logarithms with base e. Hence, the inverse of e is LN.
On your own…Home
Problems 1 to 42 page 116 (problems 1 to 42, page 119, 10th edition).
Problems 53 to 60 page 117 (problems 53 to 60, page 119, 10th edition).
|



 while
while
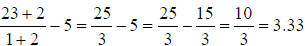
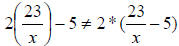

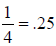 , we divide something in four
parts and each part is a quarter.
, we divide something in four
parts and each part is a quarter. , we divide something in two parts
and each part is a half.
, we divide something in two parts
and each part is a half.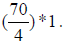
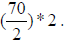
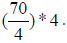
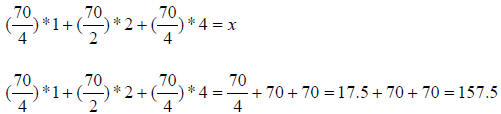
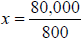 or also, x = 100.
or also, x = 100.
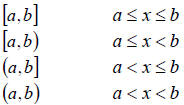


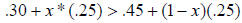

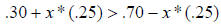
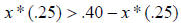
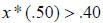
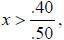 or also
or also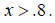

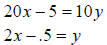
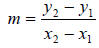
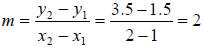
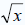 . For
. For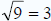 ,
because 32 = 3*3 = 9 . Square roots often
,
because 32 = 3*3 = 9 . Square roots often
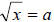 (which is called the
(which is called the (the negative of
the principal square root). For
(the negative of
the principal square root). For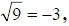 , this because while (3)*(3) = 9, we
also have that
, this because while (3)*(3) = 9, we
also have that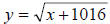
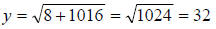
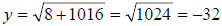
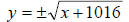
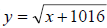 and
and 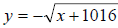 ). Thus, this
). Thus, this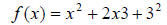


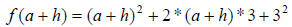
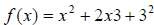 as f (x) = (x + 3)2 . Let’s
as f (x) = (x + 3)2 . Let’s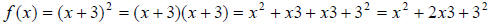
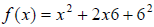 estimate the
following:
estimate the
following:
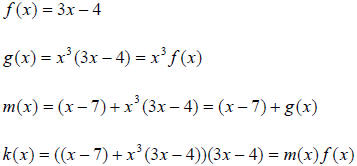
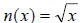
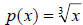
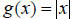
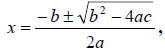 where b2 −
4ac ≥ 0 .
where b2 −
4ac ≥ 0 .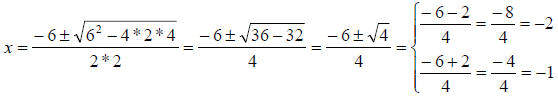
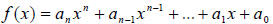
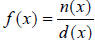


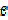 is an irrational
is an irrational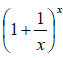
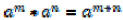
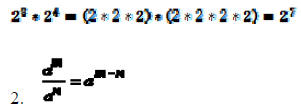
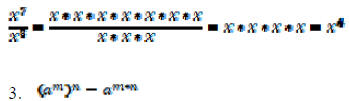
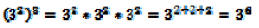
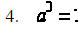

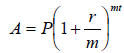

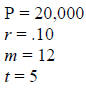
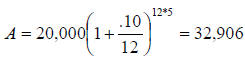
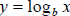
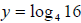 the exponential form is 16 = 4y ,
which by the way implies that y = 2.
the exponential form is 16 = 4y ,
which by the way implies that y = 2.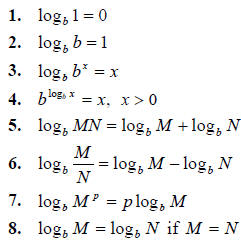
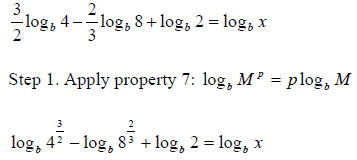
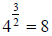 and
and