Teaching Inequalities:A Hypothetical Classroom Case
Pre-case exercises:
1. Solve the inequality 3 + 1 ≤ 7 without performing any
operations that re-arrange the
terms in the existing inequality. Instead, use a number line as a tool to solve
the problem.
2. Describe how 3 + 1 ≤ 7 is similar to 3x + 1 = 7. Describe how they are
different.
3. How is the solution to −3 + 1 ≤ 7 different from the solution to 3 + 1 ≤ 7?
Why?
4. Write a word problem for the inequality 3 + 1 ≤ 7.
Scenario:
Mr. Smith is looking for ways to get his class to
understand inequalities. He has been unhappy
with his past practices, but he has not been sure what he should change in order
to help deepen
students’ understanding. He has approached you, as a colleague who teaches
mathematics, to observe
one of his lessons and give him some feedback on his teaching. You have agreed
to do an observation
for him. The next section describes some of the events that occurred during the
lesson you observed. As
you read through the following set of events, write down some thoughts that you
might share with Mr.
Smith when you sit down with him to discuss the lesson after school that day.
The lesson:
As Mr. Smith’s students entered the room, they found a set
of warm-up exercises on the board.
Students were to solve the following five equations in the warm-up: (i) 3(x + 1)
= 21, (ii) 3(a - 3) = 2(a +
4), (iii) 3(y - 3) = 6, (iv) 3(a - 1) = 4(a - 15), (v) 2(2w + 5) + 2w = 46.
After a few minutes of class work time,
Mr. Smith asked five students to come up to the board to solve each of the
equations. When the
students had finished writing their work on the board, Mr. Smith asked if there
were any questions.
When no one asked any questions, he decided it would be OK to move on to the
next portion of the
lesson.
Mr. Smith began the next portion of the lesson by asking
students, “What do you think of when I
say the word ‘inequality’?” Several students shot their hands up to volunteer
responses. Some of the
student responses included:
· “It is a Pac-man between two numbers”
· “It is like an equation but it has a pointy symbol instead of an equal sign”
· “You do an inequality almost like how you do an equation”
· “You can solve an equation but not an inequality”
especially annoyed with the fact that students referred to
the inequality sign as a “Pac-man” rather than
using its proper name. He decided to give them some simple examples of uses
inequality signs. He said,
“In the United States, you have to be at least 18 years old to vote. We could
represent that with an
inequality symbol by writing, you ≥ 18.” Mr. Smith went on to give another
example, “This semester,
you will get at most 250 reward tickets from me for being good in class. 250 is
the maximum any one
person can get. We could represent that with an inequality symbol by writing,
you ≤ 250.” He then
went on to point out that when a problem contains the phrase “at least,” you
should use the “≥” sign,
and when a problem contains the phrase “at most,” you should use the “ ≤” sign.
Next, Mr. Smith asked students to work in groups of four
to solve some problems. He said, “Imagine
that there are 15 students who all want to earn money by putting in hours
working at the school store
this week. The school can pay for at most 60 total hours this week. How many
hours should each person
work if the hours are split fairly?” He then put the inequality 15h ≤ 60 up on
the overhead projector and
then asked students to solve and graph it. Students had solved inequalities the
previous year, so some of
them knew that graphing inequalities had something to do with open dots, closed
dots, and arrows on a
number line. Mr. Smith circulated about the room as the groups worked in order
to remind them of
when to use open dots and closed dots. As he circulated, he told them that the
arrow on the graph
should point in the same direction as the arrow in the inequality sentence (so
the arrow on the graph of
15h ≤ 60would point to the left).
When most of the groups had finished working on the
inequality on the overhead projector, Mr.
Smith called the class back together so they could watch one of the students,
Keisha, solve it for
everyone. Keisha drew a number line on the transparency, put a closed dot on the
four, and then drew
an arrow coming from the dot and going to the left. When Mr. Smith asked the
student to explain her
thinking, she said, “First, I pretended that there was an ‘=’ sign between the
15h and the 60 so I could
treat it like an equation. Then I divided both sides by 15. I got h ≤ 4. That
means each student can work
at most 4 hours each, because ′ ≤ ′ means ‘at most.’ Then I put a solid dot on
the four because there is a
line underneath the ‘at most’ symbol. Then I drew an arrow to the left because
the ‘at most’ symbol is
pointing to the left.” Pleased that Keisha had talked so much about how she
solved the problem, Mr.
Smith thought it would be good to give the students a more challenging problem.
Mr. Smith put the inequality
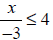 on the overhead next. He asked students to
work with their on the overhead next. He asked students to
work with their
groups again in order to solve and graph it. They quickly came up with the
solution x ≤ −12. Mr. Smith
called a student, Jasmine, up to the overhead projector to graph the solution.
She drew a number line,
put a solid dot on the 12, and then drew an arrow to the left. After Jasmine sat
back down, Mr. Smith
went up to the graph she had drawn pointed to “-15” on the number line. He asked
students to put
“-15” in for x in the original inequality. When students did so, they got 5 ≤ 4.
When Mr. Smith asked
students if it was true that 5 is less than or equal to 4, a few said “no.” He
asked them to talk in their
groups for a few minutes about what had happened in this situation. After
students spent a few minutes
squirming in their seats and talking about who had been voted off of American
Idol the previous night,
Mr. Smith asked the class to quiet down, and to direct their attention back
toward him. He wrote on the
overhead projector, “When you divide or multiply by a negative in an inequality,
you need to flip the
sign.” He told students to write the rule in their notebooks, because they would
be using it for
homework. As he was writing on the projector, the bell signaling the end of the
class period rang. He
quickly wrote the homework assignment on the projector, and told students to
copy it down before
leaving class.
Questions for reflection and discussion:
1. What were the strongest points of Mr. Smith’s lesson?
What were the weakest points?
2. Do you think that Mr. Smith’s warm-up activity was a
good lead-in to the concepts he was trying
to teach in the main portion of the lesson? Why or why not?
3. Do Mr. Smith’s students accurately reflect the way that
most students think about inequalities?
Why or why not?
4. Does Mr. Smith’s rule about translating the phrases “at
least” and “at most” into inequality
symbols work all of the time? Why or why not?
5. Was Mr. Smith’s example of 15 students working in the
school store a good word problem to
use to illustrate 15h ≤ 60 ? Why or why not?
6. Critique Mr. Smith’s approach to teaching (or
reminding) students how to graph inequalities.
7. Critique Keisha’s work on the problem she demonstrated
at the front of the room.
8. Critique Mr. Smith’s use of group work. Was his use of
group work appropriate for this lesson?
Why or why not?
9. What steps could Mr. Smith have taken in order to lead
students toward discovering the rule for
“flipping” an inequality sign when multiplying or dividing by a negative?
10. Mr. Smith made extensive use of the overhead projector
during this lesson. What are the
advantages and disadvantages of using an overhead projector as a teaching tool?
11. Do you think that Mr. Smith’s students will retain the
material they learned during this lesson
for a long period of time? Why or why not?
12. What should students know about inequalities at
various different grade levels (grades 5-8)?
How can teachers build on what students learn about inequalities at each grade
level?
|


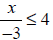 on the overhead next. He asked students to
work with their
on the overhead next. He asked students to
work with their