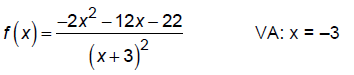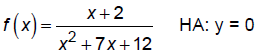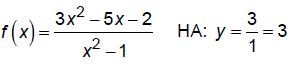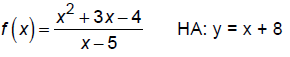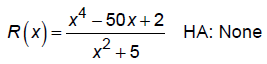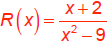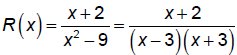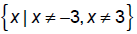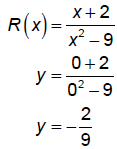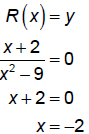Home
Linear Equations and Inequalitie
Solving Inequalities
Absolute Value Inequalities
Graphing Equivalent Fractions Lesson Plan
Investigating Liner Equations Using Graphing Calculator
Graphically solving a System of two Linear Equatio
Shifting Reflecting Sketching Graph
Graphs of Rational Functions
Systems of Equations and Inequalities
Graphing Systems of Linear Equat
LINEAR FUNCTIONS: SLOPE, GRAPHS AND MODELS
Solving Inequalities with Absolute Values
Solving Inequalities
Solving Equations & Inequalities
Graph the rational function
Inequalities and Applications
Inequalities
Using MATLAB to Solve Linear Inequalities
Equations and Inequalities
Graph Linear Inequalities in Two Variables
Solving Equations & Inequalities
Teaching Inequalities:A Hypothetical Classroom Case
Graphing Linear Inequalities and Systems of Inequalities
Inequalities and Applications
Solving Inequalities
Quadratic Inequalities
Inequalities
Solving Systems of Linear Equations by Graphing
Systems of Equations and Inequalities
Graphing Linear Inequalities
Inequalities
Solving Inequalities
Solving Inequalities
Solving Equations Algebraically and Graphically
Graphing Linear Equations
Solving Linear Equations and Inequalities Practice Problems
Graphing Linear Inequalities
Equations and Inequalities
Solving Inequalities

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Graphs of Rational Functions

Summarize asymptotes from last time. Vertical Asymptote: Find zeros of denominator. VA are x = k

Horizontal Asymptote: [degree numerator] < [degree denominator]	y = 0

[degree numerator] = [degree denominator]	y = L (ratio of coefficients of dominant terms)

[degree numerator] = [degree denominator] + 1	y = mx + b (find by long division)

[degree numerator] > [degree denominator] + 1	no linear asymptotes

Section 4.3 Graphs of Rational Functions

Now, we will graph rational functions. This process is a bit different from the one in the book ut I think
it is easier to do:

1. Factor, state domain, and THEN reduce.
2. Plot intercepts. For x-intercepts, state whether graph touches (multiplicity is even) or
crosses (multiplicity is odd) x-axis.
3. Draw vertical asymptotes (the zeros of the denominator).
4. Draw horizontal asymptotes:

If deg num < deg denom, y = 0 is a horizontal asymptote
If deg num = deg denom, y = L is a horizontal asymptote
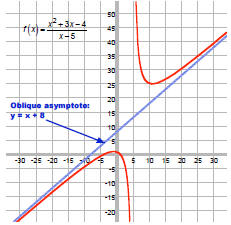
If deg num = deg denom + 1, use long division to find oblique asymptote, y = mx + b
5. Plot where the graph crosses a horizontal or oblique asymptote, if it does. That is, solve
the equation:
Function = asymptote
R(x) = y
6. If needed, plot a few extra points.
7. Connect the dots.

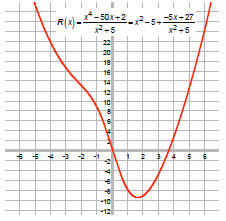
Ex: Graph

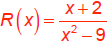
1. Factor, state domain, and THEN reduce.

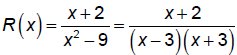
Domain: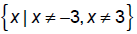

Cannot reduce.

2. Plot intercepts. For x-intercepts, state whether graph touches (multiplicity is even) or
crosses (multiplicity is odd) x-axis.
x-intercept:

The factor x + 2 has multiplicity 1, which is odd, so graph crosses here.
y-intercept:

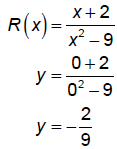
3. Draw vertical asymptotes (the zeros of the denominator).
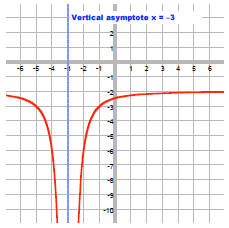
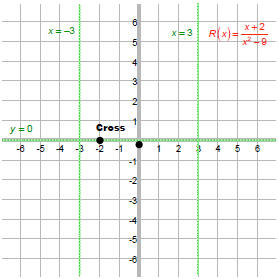
These occur when the denominator is 0. That is, at x = -3 and x = 3.

4. Draw horizontal asymptotes:
Since deg num < deg denom, HA is y = 0

5. Plot where the graph crosses a horizontal or oblique asymptote, if it does. That is, solve
the equation:

Solve R(x) = y

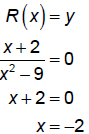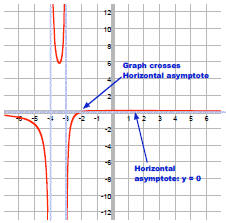
So, the graph crosses the horizontal asymptote at x = –2.

6. If needed, plot a few extra points.
R(-4) = -0.3
R(4) = 0.9

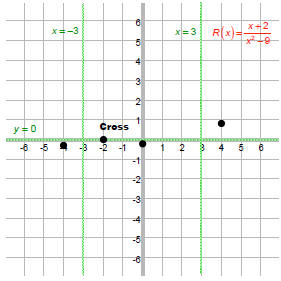
7. Connect the dots.
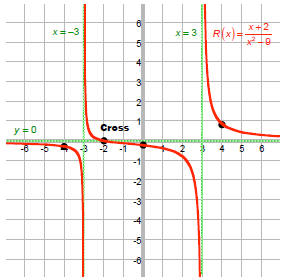