Solving Systems of Linear Equations
Solving Systems of Linear Equations by Graphing
Learning Objectives:
1. Decide whether an ordered pair is a solution of a
linear system.
2. Solve systems of linear equations by graphing.
3. Use graphing to identify systems with no solution or infinitely many
solutions.
4. Use graphs of linear systems to solve problems.
Examples:
1. Consider the system.
x + y = –3
2x + y = 1
Determine if each ordered pair is a solution of the
system.
a. (4, 7)
b. (4, –7)
2. Solve the following systems by graphing. State the
solution (the intersection point) as an
ordered pair (x, y) or state if there is no solution, or state if there are an
infinite number of
solutions.
a.
2x + y = –3
y = –2x –3
b.
2x + y = 3
3x – 2y = 8
c.
x + 2y = 6
x + 2y = 2
Teaching Notes:
• When graphing a system of linear equations, there
are three possible outcomes:
1. The two lines can intersect at one point, meaning there is one
solution to the system.
2. The two lines can be parallel to one another, meaning there is no
solution to the system.
3. The two lines are identical or coincide, meaning there are infinitely
many solutions to the system.
• When two lines are parallel the system is inconsistent and has no
solution.
• When two lines are coinciding, they are called dependent equations and
have infinitely many solutions.
Answers:
1.
a. not a solution
b. yes, a solution
2.
a. infinitely many solutions
b. (2, –1)
c. lines parallel, no solution
Solving Systems of Linear Equations by the Substitution
Method
Learning Objectives:
1. Solve linear systems by the substitution method.
2. Use the substitution method to identify systems with no solution or
infinitely many solutions.
3. Solve problems using the substitution method.
Examples:
Solve each system using the substitution method. If there
is no solution or an infinite number of
solutions, so state.
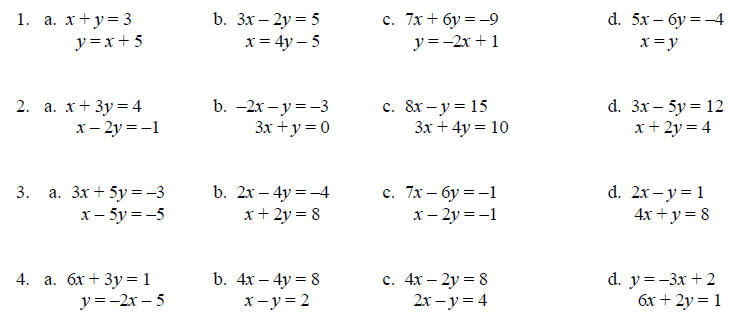
Teaching Notes:
• Students like to follow specific steps so give
them a list of steps to use for solving systems
by substitution. Begin with: Isolate a variable with a coefficient of 1 first.
• Many students think they must solve for y. Stress that it does not
matter whether the variable
solved for is x or y.
• Use colored pens or markers to underline in one equation what will be
substituted in the
other equation.
• If a graphing calculator is being used in the class, graphing on the
calculator is a good way
to check solutions.
Answers: 1. a. (–1, 4) b. (3, 2) c. (3, –5) D. (4,
4) 2. a. (1, 1) b. (–3, 9) c. (2, 1) d. (4, 0)
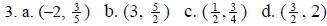 4. a. No solution b.
Infinite solutions 4. a. No solution b.
Infinite solutions
c. Infinite solutions d. No solution
Solving Systems of Linear Equations by the Addition
Method
Learning Objectives:
1. Solving linear systems by the addition method.
2. Use the addition method to identify systems with no solution or
infinitely many solutions.
3. Determine the most efficient method for solving a linear system.
Examples:
Solve the following systems by the addition method.
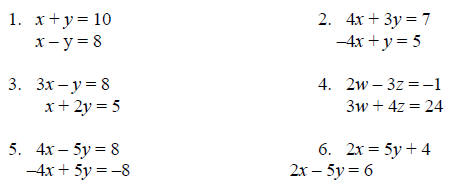
Teaching Notes:
• When solving a system of linear equations there are three methods:
Graphing (5.1)
Substitution (5.2)
Addition (5.3)
• Any of the three methods will work when solving a system and produce the
correct
answer.
• Teach students how to determine which of the three methods is the most
efficient when
solving a system of equations.
Answers: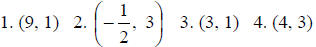 5.
infinitely many solutions 6. no solution 5.
infinitely many solutions 6. no solution
|


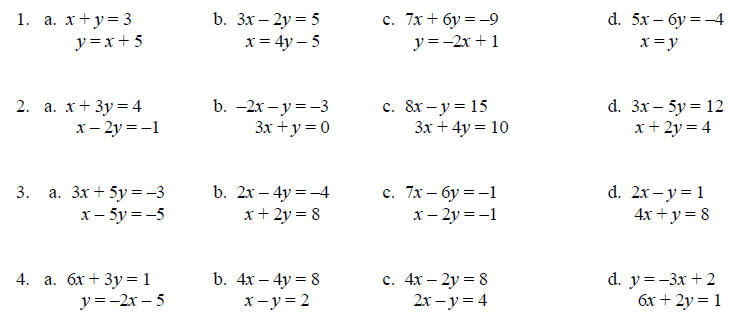
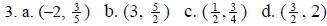 4. a. No solution b.
Infinite solutions
4. a. No solution b.
Infinite solutions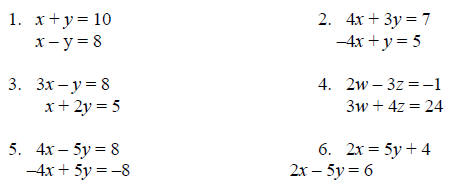
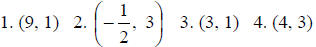 5.
infinitely many solutions 6. no solution
5.
infinitely many solutions 6. no solution