|
|
Graphing Systems of Linear Equations
Lesson Title: A Point of Intersection
Draft Date: 6/17/08
1st Author (Writer): Jenn Spiess
2nd Author (Editor/Resource Finder): Rachael Neurath
Algebra Topic: Graphing Systems of Linear Equations.
Grade Level: 6-10
Cartoon Illustration Idea:
1. Two robots with lines trailing behind them on a grid (like the ground) both
claiming: “Hey,
that’s my point!” “No, it’s mine”
Outline of Lesson
Content (what is taught):
• Solving systems of linear equations by graphing
o Definition of a solution to linear system with two equations
o Review graphing of a linear equation
o Review writing linear equations from a graph
Context (how it is taught):
• Two robots are driven across a grid dragging a string behind them.
• The solution to the system is identified.
• The solution to the system is verified algebraically.
Activity Description:
Robots will be equipped with a string to be dragged behind the robot across a
grid to create a system of
two lines. Students will estimate the solution (point where the lines meet),
write the equations of the
lines drawn if they are not provided (prior knowledge), verify that the solution
satisfies both equations
algebraically.
Standards: (At least one standard each for Math, Science, and Technology
- use standards provided)
• Math – B1, B2, B3
• Technology – F1, A3
Materials List:
• Two robots per group
• Large grid on the ground per group
• String for each robot
• Copy of worksheet for each group or person
ASKING Questions
Summary:
Discuss the concept of a solution to a system of two linear equations
graphically.
Outline:
• Using two rulers to represent lines, hold them up to show two intersecting
lines
• Ask questions to help students identify the number of solutions possible in a
system (one, none,
or many)
• This lesson focuses only on systems with one solution.
| Questions |
Possible Answers |
Questions Possible Answers
1. A system of equations is made up of two or more equations…
let’s start with just two for now. Holding up two rulers that cross
forming an X: Do these two lines meet? |
1. Yes. |
2. If these lines were on a grid, the spot where
they meet would be
called what? (May need to prod some here… Is it a line?) |
2. A point. |
| 3. What do we know about points? |
3. There’s an x and a y value. |
| 4. Is a point always made up of nice numbers like
(2, 3)? |
4. No. |
| 5. What could it look like then? |
5. Sample (2.75, 3.1).
Answers may vary. |
6. Ask students to identify the
solution to various systems. Use
either resource listed. |
6. Answers will vary. |
Image Idea:
1. Teacher holding two rulers to demonstrate intersecting lines in front of a
class.
2. Screen shot of either site? Not sure of copyright on this…
EXPLORING Concepts
Summary:
Students explore that a single point satisfies two equations, and is therefore
the solution to the system
of equations.
Outline:
• Groups use robots to draw system
• Rest of class identifies the solution
• Split class to each verify the solution in one of the two equations
• Rotate and repeat
Activity:
Have a group of three or four students “draw” specific equations/lines on a
large grid on floor with the
robots dragging the string behind and have a student stand at the “solution”.
The rest of the class should then identify the solution/point. Split this larger
group in two and assign
each group to algebraically determine whether the solution worked one of the two
equations. Students
should discover that the point “works” for either equation.
Rotate groups so each group is up out of their seats to create the graph once
and algebraically verifying
solutions multiple times. Another station could be added where students use the
Classzone animation
Chapter 7: Solve by Graphing to see these concepts in another format.
Resources
• See Chapter 7: Solve by Graphing animation from Classzone This animation can
also be
used to show students that the solution satisfies both equations. Check the box
to show the
algebraic check. Students drag the green dot around the grid.
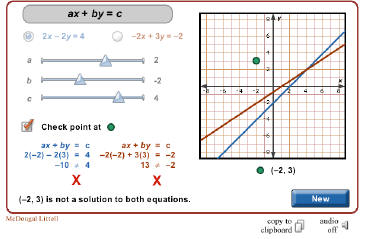
Image Idea:
1. Students standing at the solution
INSTRUCTING Concepts
This portion will be provided by the Instructional Writing Team.
ORGANIZING Learning
Summary:
Groups of students will use the robots to draw the two lines of a system,
determine its solution, and
verify the solution in both equations.
Outline:
• Draw given lines with robots.
• Record on worksheet.
• Identify solution.
• Algebraically verify the solution in both equations.
• Students will verify graphs and solutions using graphing calculators
Activity:
A worksheet requiring students to graph two different lines using the robots,
and record their graphs
will be provided. It will also ask them to write the equations of both lines,
estimate the solution to the
system, and verify the solution satisfies both equations.
Worksheet Idea:
• Three problems:
o Two regular systems, (perhaps one with a decimal solution).
o Third problem where students can create their own system, where they draw the
lines,
write the equations, find the solution, and verify it.
• Each problem has a grid to record the graph, and a place to write and verify
the solution.
UNDERSTANDING Learning
Summary:
Students write a description of how to solve a system of equations by graphing.
Outline:
• Formative assessment of solving a system of equations by graphing.
• Summative assessment of solving a system of equations by graphing.
Activity:
Formative Assessment
As students are engaged in learning activities ask yourself or the students
these types of questions:
1. Were students able to graph both lines successfully?
2. Were students able to estimate the solution successfully?
3. Can students explain how to verify a solution algebraically?
Summative Assessment
A. In a written or verbal interview with the teacher, students will describe how
to graph each line in a
system and determine the solution to the system. They should also describe
whether or not the
solution is correct algebraically.
B. Ask students to write their own word problem(s) using graphing systems to
solve a problem.
C. Students should be able to answer the following quiz questions:
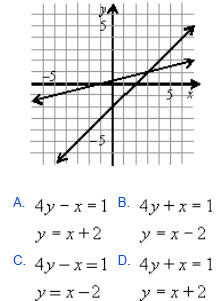
1. The solution to which system is shown by the following graph? (Answer: C)
2. Destiny is renting a bicycle for a day. She has two options for renting the
bicycle as shown in
the following chart.
| Rent Option |
Deposit |
Price Per Hour |
Equation |
| A |
$10 |
$4 |
(C = 4x + 10) |
| B |
$15 |
$2 |
(C = 2x + 15) |
a - b. Write an equation that shows the total cost for
each option.
c. When will the two options cost the same amount? (2.5 hours)
d. If she plans to ride for two hours, which is the best option? (A)
e. If she plans to ride for five hours, which is the best option? (B)
|



