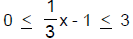|
Home |
Solving InequalitiesChapter 1.1 Expressions and Formulas Evaluate:
9. What is the sum of -14 and -7? 10. What is the difference of 4 and -7? 11. What is the product of -16 and 3? 12. What is the quotient of 16 and 4/3? Solve for the indicated variable: 14. Solve for L: S = L - rL 15. Solve for C: P = R - C 16. Solve for A: Chapter 1.2 Properties of Real Numbers Name the sets of numbers that contain each number listed
below. Use natural (N), whole (W),
State the property of real numbers that is illustrated in each equation.
Write in decreasing order.
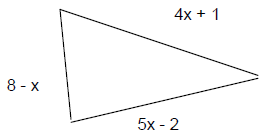
Simplify: 18. 10 - [ 8 (5 - x) + 2 ] 19. 8(r + 7t) - 4(13t + 5r) 20. 0.25(6 + 20y) - 0.5(19 - 8y) Chapter 1.3 Solving Equations Write an algebraic expression or equation to represent each verbal expression. 1. 7 more than the product of a number and 10 Solve these equations. 8. 0.5x - 12 = 4 9. 5x - 4 = 2x + 6 10. 2 (3 - x) = 16 (x + 1) 11. 7 (x + 1) = 1 - 2 (5 - x) 12. - (x - 1) + 10 = - 3 (x - 2 13. Find the dimensions of the figure 4x + 1
14. The bill for the repair of your car was $415. The cost
for parts was $265. The cost for 15. The maximum speed of a 1991 Case tractor is 19.6 miles
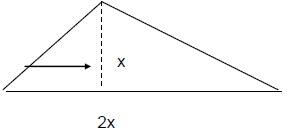
per hour, which is 1.2 more First, find an algebraic expression for the area of the
figure. Then determine the actual area using 16. a = 5, b = 4
17. x = 9
Chapter 1.5 Solving Inequalities Write the correct inequality symbol between the numbers. Graph on a number line. Solve the inequality. Chapter 2.1 Relations and Functions For each set of points, identify the domain, the range,
and tell whether it is a function or not. 2. {(1,2), (2, 3), (2, 5), (1, 6)} 3. {(4, 5), (5, 4), (6, 5), (5, 6)} 4. {(1, 4), (2, 8), (3, 12), (-1, -4), (1, 4)}
6.
Given the functions f (x) = 2x2 + 3x - 5 and g (x) = 4x -
2, evaluate the following: |


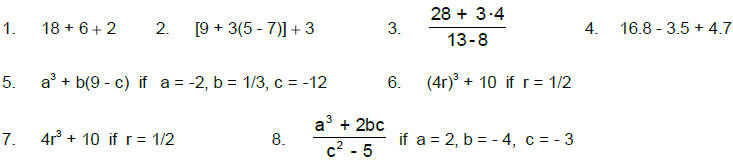




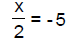
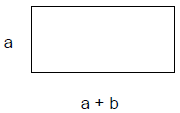
 ≥ 15
≥ 15