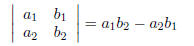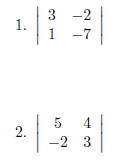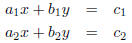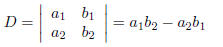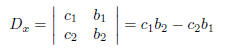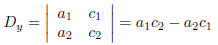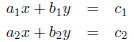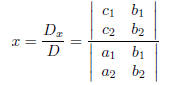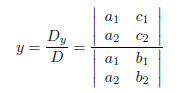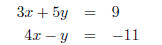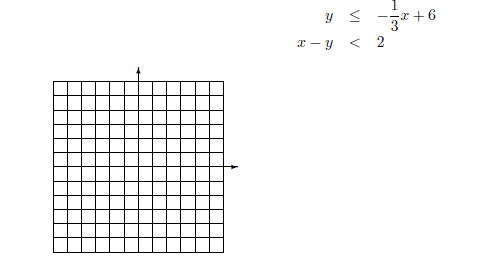|
Home |
Systems of Equations and Inequalities4.1 Solving Systems of equations in Two VariablesDe nition 1. A system of linear equations is two or more linear
equations to which we try to EX 1. Consider the equations:
A solution to a system of linear equtions is an ordered pair or pairs
that satisfy ALL equations 4.1.1 Solve Systems of Linear Equations Graphically To solve a system with two equations in two variables we graph them both on
the same axes and EX 2. - 1. Solve the following system of equations graphically.
2. Let's consider all the possible ways that two lines can interact:
4.1.2 Solving Systems by Substitution It is usually not practical to solve systems by graphing (messy drawings,
points may not be exactly Substitution Method 1. Pick an equation and solve for one of the variables. (Note: It is usually
easiest to solve for a EX 3. - 1. Solve using the substitution method.
2. Solve using the substitution method.
4.1.3 Solving Systems Using the Addition Method Often the easiest method for solving a system of equations is the addition
method (also known as EX 4. Solve the following system of equations using the addition method.
Addition Method 1. If necessary, rewrite each equation in standard form. EX 5. - 1. Solve using the addition method:
2. Solve using the addition method:
3. Solve using the addition method:
4. Solve using the addition method:
4.2 Solving Systems of Linear Equations in Three VariablesAn equation of the form 3x - 2y + 4z = 11 is a linear equation in three
variables. The solution EX 6. - 1. Solve the following system using the substitution method.
2. Solve the following system using the addition method.
3. Solve the following system using the addition method.
4.3 Applications and Problem SolvingThere are countless applications for systems of equations. We will examine a couple examples EX 7. - 1. How many pints of a 10% salt solution and a 50% salt solution must be
combined to get 44
2. On an algebra test, a total of 75 students had grades of A or B. There
were 5 more students
3. Three brothers invest a total of $35,000 a business. The rst brother earns
3% pro t on his
4.4 Solving Systems of Equations Using Matrices4.4.1 Matrices A matrix is a rectangular array of numbers within brackets. The plural of
matrix is matrices.
The numbers inside the matrices are referred to as elements. We refer to the
size of the matrix
the corresponding matrix is written:
EX 9. Express the following system of linear equations with an augmented matrix.
4.4.2 Solve Systems of Linear Equations In order to solve systems of equations using matrices we will attempt to
transform our matrices using
To transform a matrix into this form we have the following row transformations: Procedures for Row Transformations 1. Any row may be multiplied (or divided) by a nonzero number. EX 10. - 1. Solve the following system of equations using matrices.
2. Solve the following system of equations using matrices.
3. Solve the following system of equations using matrices.
4.4.3 Recognize Inconsistent and Dependent Systems Recall that we call a system of equations inconsistent if there are no common
solution to the Let's examine how to determine, using matrices, if a system is inconsistent or dependent. EX 11. - 1. Solve the system of equations using matrices.
2. Solve the system of equations using matrices.
4.5 Determinants and Cramer's Rule4.5.1 Evaluate a Determinant of a 2*2 Matrix For every 2*2 matrix we can find a number associated with it called the determinant. The determinant of a 2*2 matrix
EX 12. Evaluate the following determinants:
4.5.2 Cramer's Rule We will study now a cool rule that gives us a formula for solving systems of
linear equations. We Given the system of equations:
We denote by D the following:
Further we denote with Dx and Dy:
and
Finally, we have Cramer's Rule: For the system of equations
Then the solution is given by
and
EX 13. Solve the system of equations using Cramer's rule.
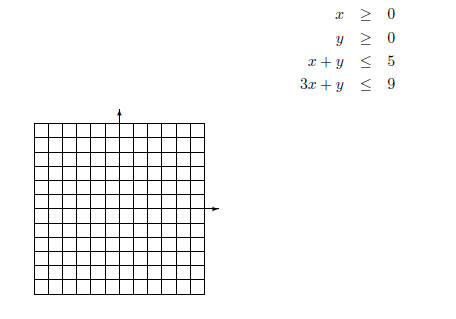
REMARK 1. When D = 0: 4.6 Solving Systems of Linear InequalitiesRecall, we learned how to graph linear inequalities in two variables: EX 14. Graph the inequality 2x + 3y > 6
We now investigate how to solve systems of linear
inequalities graphically. EX 15. -
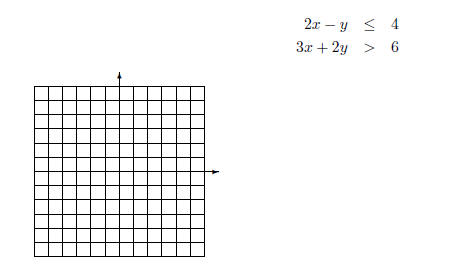
2. Graph
3. Graph
|



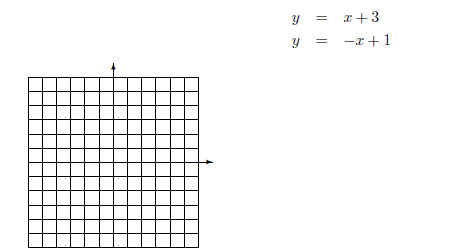

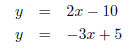
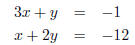
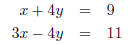
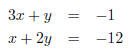
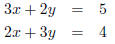
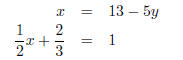
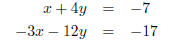
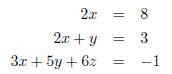
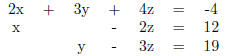
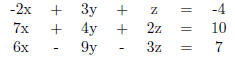
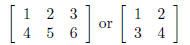
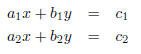
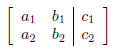
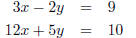
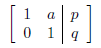
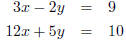

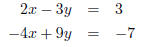


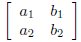 is denoted
is denoted