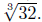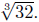Solving Equations & Inequalities
7.10. Solution: Solve for y in yx2 − 2x − 4y2 = 0. The first thing to
do is to rearrange the equation:
−4y2 + x2y − 2x = 0
Now we can see that a = −4, b = x2, and c = −2x.
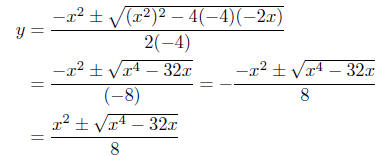
Presentation of Solutions:
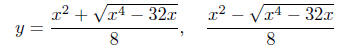
Comments: We get real solutions when x is such that x4 − 32x ≥ 0.
This problem will be continued in the section on Solving Inequalities.
7.11. Solution to (a): Begin by rearranging the equation in the form
of a quadratic in w:
5wx4 − 2w2x2 +3 = 0
becomes
(−2x2)w2 + (5x4)w + 3
Now it is apparent that a = −2x2, b = 5x4, and c = 3.
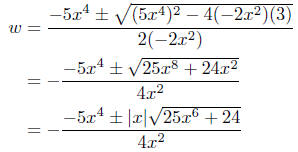
Now here’s an interesting simplification. How to remove the absolute
value? If x ≥ 0, the |x| = x; if x < 0, then |x| = −x. The second case
has the effect of changing ‘±’ (plus or minus) to ‘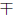 ’ (minus or plus). ’ (minus or plus).
So I think it is safe to remove the absolute value—it will not change
the solutions. Therefore,
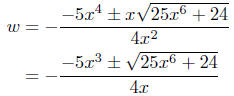
Now x is a factor common to both the numerator and denominator—
we can and do cancel it.
Presentation of Answer: 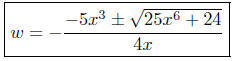
Did you get it?
Solution to (b): Solve for x2 in 5wx4 − 2w2x2 +3 = 0.
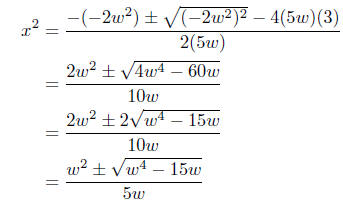
Presentation of Solution:
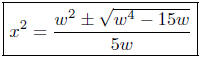 (A-1) (A-1)
Comments: Real solutions exist provided w4 − 15w ≥ 0. When we
take up solving inequalities, we’ll return to this problem to do a more
detailed analysis of it. Suffice it to say that solutions exist for x2
provided (1) w4 − 15w ≥ 0 and (2) the right-hand side of (A-1) must
be nonnegative as well.
Exact conditions under which this equation has solution for x2 can be
made after we analyze some inequalities . . . later.
7.12. Solutions:
(a) Solve for x: 4x + 12 ≤ 5.
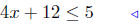 |
given |
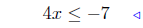 |
add −12 to both sides (10) |
 |
multiply both sides by 1/4: see (11) |
Presentation of Answer. Interval Notation: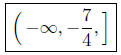
(b) Solve for x: 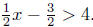
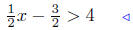 |
given |
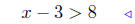 |
multiply both sides by 2: (11) |
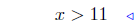 |
add 3 to both sides: see: (10) |
Presentation of Answer. Interval Notation:
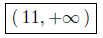
(c) Solve for x: 3 − 8x ≥ 4
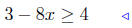 |
given |
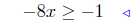 |
add −3 to both sides: (10) |
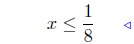 |
inequality reversed! See: (12) |
Presentation of Answer. Interval Notation: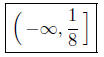
7.13. Solutons:
(a) Solve for x: 2x − 1 ≤ 5x + 2.
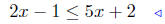 |
given |
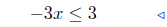 |
add 1 − 5x to both sides |
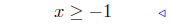 |
inequality reversed: (12) |
Presentation of Answer:
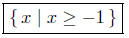
(b) Solve for x: 3x + 4 > 1 − 6x.
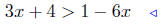 |
given |
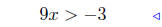 |
add 6x − 4 to both sides: (10) |
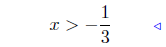 |
inequalities not reversed: (10) |
Presentation of Answer: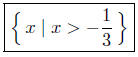
7.14. Solutions:
(a) Solve for x: 3 < 2x + 1 ≤ 12.
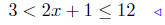 |
given |
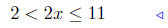 |
add −1 to all sides |
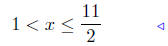 |
multiply 1/2 on all sides |
Presentation of Answer: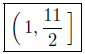
(b) Solve for x: −2 ≤ 2 − 5x ≤ −1.
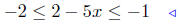 |
|
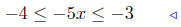 |
given |
 |
add −2 to all sides |
Presentation of Answer: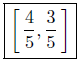
(c) Solve for 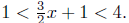
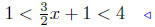 |
given |
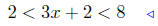 |
multiply all sides by 2 |
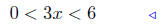 |
add −2 to all sides |
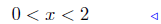 |
multiply all sides by 1/3 |
Presentation of Answer:
7.15. Solutions to(a): Solve for x: x2−x−2 ≤ 0. Begin byfactoring
the quadratic.
(x + 1)(x − 2) ≤ 0
Now, do a Sign Chart Analysis.
The Sign Chart of (x + 1)(x − 2)

Presentation of Solution. Interval Notation: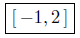
Set Notation: 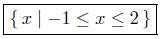
Comments: We include the endpoints in the solution because they
would satisfy the inequality—that’s a good reason!
Solution to (b): Solve for x: x3 − 4x2 + 3x > 0. Begin byfactoring
completely:
x(x − 1)(x − 3) > 0.
The Sign Chart of x(x − 1)(x − 3)

Presentation of Solution. Interval Notation: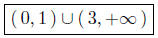
Set Notation: 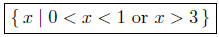
Comments: Here, we do not include the endpoints. At the endpoints,
the expression is zero, which does not satisfythe inequality.
7.16. Solution to (a): Solve for x in x2 − 3x ≤ 4. Begin bytaking
the 4 to the left-hand side of the inequality,
x2 − 3x − 4 ≤ 0.
Now factor,
(x + 1)(x − 4) ≤ 0.
Now do a Sign Chart for (x + 1)(x − 4).
The Sign Chart of (x + 1)(x − 4)

Presentation of Solution: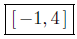
Solution to (b): Solve for x in 6x − x2 < 5. Therefore,
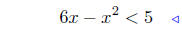 |
given |
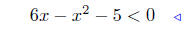 |
put everything to l.h.s. |
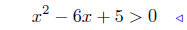 |
multiply by −1: I didn’t like the −x2 |
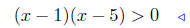 |
now factor! |
Now do a Sign Chart for (x − 1)(x − 5).
The Sign Chart of (x − 1)(x − 5)

Presentation of Solution:
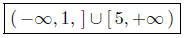
7.17. Solution to (a): Solve 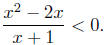
Begin byfactoring: 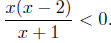 Now do a Sign Chart. Now do a Sign Chart.
The Sign Chart of 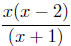

Presentation of Solution: Solve 
Set Notation: { x | x < −1 or 0 < x < 2 }
Interval Notation: (−∞,−1 ) ∪ ( 0, 2 )
Solution to (b): Solve for 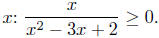
Begin by factoring,
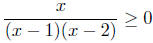
It is this inequality we solve using the Sign Chart Method.
The Sign Chart of 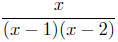

Presentation of Solution: Solve 
Set Notation: { x | 0 ≤ x < 1 or x > 2 }
Interval Notation: [ 0, 1 ) ∪ ( 2,+∞)
We include x = 0 in the solution because this point makes the expression
0; hence, x = 0 satisfies the inequality. We don’t include x = 1 or
x = 2 in the solution set because they mak e the denominator equal
to zero—a no-no.
7.18. Solution: Solve x4 − 32x ≥ 0. First factor: x(x3 − 32) ≥ 0.
The second factor can be factored some more (it is the difference in
cubes), but in this instance it would be a waste of pencil lead to do so.
The important point about the factors is that you can discern when
theyare positive and when theyare negative—we can do that for the
factor (x3 − 32).
We must ask the question, when is x3 − 32 > 0? The Answer: when
x3 > 32 or when x > 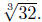 Similarly, x3 − 32 < 0
when x < Similarly, x3 − 32 < 0
when x < 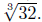
Thus, . . .
The Sign Chart of x(x3 − 32)

Presentation of Solution: Solve for x: x4 − 32x ≥ 0.
Interval Notation: 
Comments: This finally answers the question: For what values of x
does the equation
yx2 − 2x − 4y2 = 0
have real solutions for y? The answer is that x must be a number
less than or equal to 0 or a number greater than or equal to
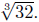
Otherwise, there are no real solutions for y.
|


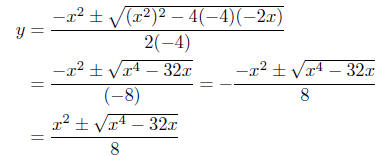
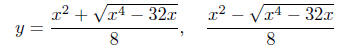
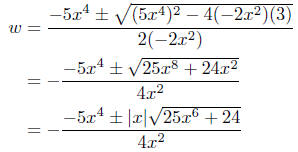
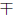 ’ (minus or plus).
’ (minus or plus).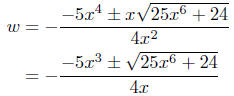
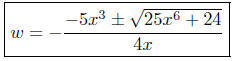
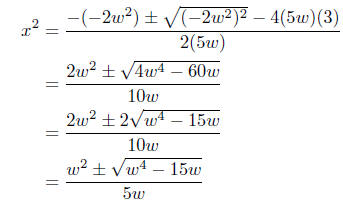
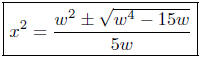 (A-1)
(A-1)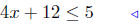
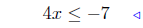

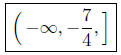
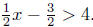
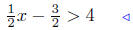
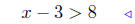
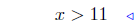
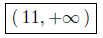
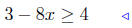
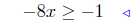
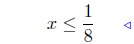
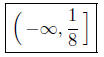
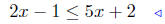
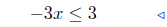
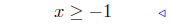
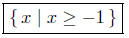
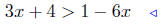
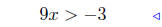
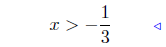
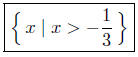
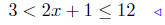
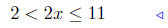
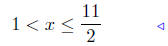
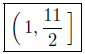
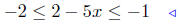
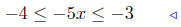

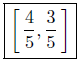
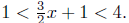
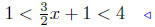
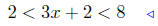
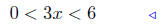
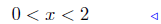


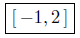
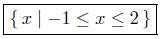

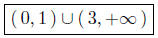
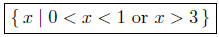

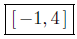
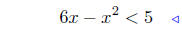
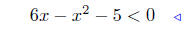
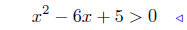
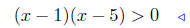

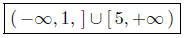
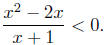
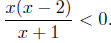 Now do a Sign Chart.
Now do a Sign Chart.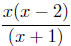


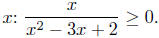
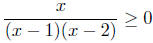
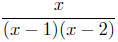


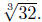 Similarly, x3 − 32 < 0
when x <
Similarly, x3 − 32 < 0
when x <